Rolling-Block Mazes Rolling-Block Mazes

		The concept of a rolling block maze was invented by Richard Tucker in the fall of 1998. Tucker is a British software developer and puzzle designer. One of his creations is the mechanical puzzle “King’s Court,” published by Pentangle. Tucker’s original maze was first presented in a column I wrote in the December 1998 Mensa Bulletin. It was also shown on my web site and, most importantly, on Ed Pegg Jr’s web site, www.mathpuzzle.com. Ed’s site created something of a craze for this type of maze. Many people began creating these mazes using blocks with ever weirder shapes. It was the sort of collaborative effort that could only happen on the Internet. I’ll discuss the development of rolling-block mazes and I will present several of them. I’ll also provide links to people who are creating more of these mazes.
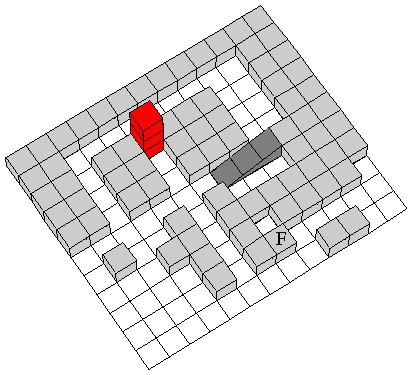
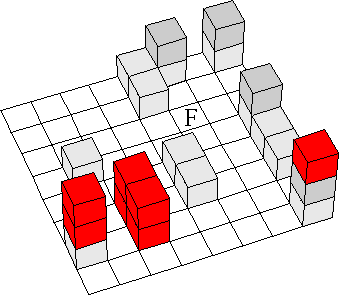
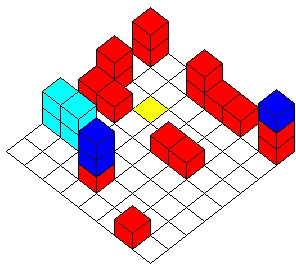
		Tucker said that he based his original maze on my rolling-cube mazes, but clearly there are a lot of differences. In a rolling-cube maze, a single die rolls from square to square, and it is the pip value on top of the die that determines where it can move. In a rolling-block maze there are no pips; it is the shape of the block that determines how it can move. The rules for these mazes are therefore simpler and clearer, though the mazes are capable of great complexity. You can click here for a page with a sampling of the older rolling-cube mazes. That page in turn has a link to a page of much older rolling-cube puzzles. This is getting complicated, so let me summarize this history: Rolling-cube puzzles were precedents to my rolling-cube mazes, and these mazes were precedents to Tucker’s rolling-block mazes.
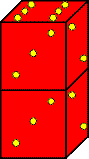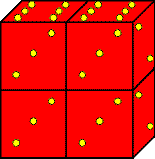
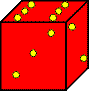
		To travel through the first four of these mazes, you’ll need a 2x1x1 block. An easy way to construct it is to take two dice and wrap them together with Scotch tape. The pips on the dice have no meaning, so it doesn’t matter which faces of the two dice you put together. Your block should look something like the picture at the left. Well, it won’t really look that bad. That’s just the best picture I can draw using MS Publisher.

Richard Tucker’s Original Rolling-Block Maze

Besides creating the block for this maze, you also have to print out a full-size diagram of the maze. You can click here to go to that diagram and then print it.

Small Version of Maze      At the left is a small illustration of the maze. The numbers in the illustration are only for the example given below. Those numbers don’t appear in the full-size diagram of the maze.
      To begin the maze, stand the block vertically on the square marked Start. You then must roll the block around the maze until it is standing vertically on the square marked Goal. At no time can any part of the block land on any of the squares with the brick wall pattern.
      Here is an example: From Start there is only one possible move, to tip the block west. It now lies horizontal and covers the square labeled Goal and the square numbered 1. The second move can only be to roll the block north, so it lies across the two squares numbered 2. On the third move you must roll the block to the east. It is now standing vertically on the square numbered 3. For the fourth move you have a choice, to tip the block to the east or to the south. And so on. Click here for the solution.

I found Tucker’s concept to be so intriguing that I wanted to create my own layout for one of these mazes. So—next we have . . .

Robert Abbott’s Rolling-Block Maze

You can click here for a diagram of the maze, then print it. The rules are the same as those in Tucker’s maze. And you can click here for the solution.

My rolling-block maze has extensive false paths and loops—something I try to have in all my mazes. Richard Tucker immediately picked up on the importance of these diversions from the true path. So—now we have . . .

Richard Tucker’s Hayling Island Maze

This rolling-block maze has the name “Hayling Island” because that’s where Tucker created it.

This is, so far, the hardest of these rolling-block mazes. After you’ve gone a short distance from Start, you’ll find yourself entangled in a thicket of interlocking loops. Even if you find your way through that thicket, more confusion lies ahead.

Click here for a diagram of the maze, then print it. The rules are the same as those in the original rolling-block maze. And you can click here for the solution.

A Rolling-Block Maze from GAMES Magazine

I talked GAMES Magazine into running a series of these mazes. Eventually they used seven, starting in the issue of May, 2002. Two of the mazes were repeats from this site—Richard Tucker’s Hayling Island maze and my first rolling-block maze. The other five were new mazes I created for the magazine.

Here is a new Rolling-Block Maze that appeared in the issue of October, 2003. Click here for the diagram, then print it. The rules are the same as those in the preceeding three rolling-block mazes. I won’t give the solution (sorry about that), and I also won’t give solutions for most of the following mazes.

By the way, everybody should subscribe to GAMES. Yeah, I know they have a lot of dumb stuff, like puzzles with celebs in them, but they’re just trying to have general appeal. Most of the stuff in GAMES is good.

Two Rolling-Slab Mazes

Ed Pegg has consistently nurtured the creation of these rolling-block mazes. Every maze in this section, plus others that I didn’t use, has appeared as a Puzzle-of-the-Week on his site. One week Ed received two Rolling-Slab mazes from two different people. Each used a shape made of four dice taped together to form a 2x2x1 slab. I think it’s pretty amazing for two people to come up with the same original idea at the same time. One maze was from maze designer Adrian Fisher and the other from Erich Friedman. Friedman is an Associate Professor of Mathematics at Stetson University, in DeLand, Florida. You might check out his puzzle page, especially the Mirror Puzzles, which have the appearance of mirror mazes.

After you’ve taped together four dice to form the slab, click here to get to Adrian Fisher’s maze, then print it. Place one of the narrow sides of the slab on the two squares marked Start. Then roll the slab around the board until you can get a narrow side to cover the two squares marked Goal. The shortest solution takes 52 moves.

Click here to get to Erich Friedman’s maze and print it, then follow the same rules. The solution to this maze takes 54 moves.

A Rolling-Slab Maze from GAMES Magazine

This maze appeared in GAMES in the issue of July, 2002. Click here for the diagram, then print it. The rules are the same as those for the other rolling-slab mazes except you start with the slab laying flat on the four squares marked Start and you must move the slab to cover the four squares marked Goal.

I’m rather proud of the layout I created for this maze, so I added a page with more information. That page also has a hint and a link to the solution.

Adrian Fisher’s Chasm Maze

This is a really great idea from maze designer Adrian Fisher.

Tape together three dice to form a 3x1x1 column. Click here to get to the maze and then print it. Place the column upright on the square marked Start and roll it around until you get it upright on the square marked Goal.

There is an interesting change of rules in this maze. The shaded squares don’t act as barriers the same way as the squares with brick patterns do in the other mazes. Here, you may not have the column upright on one of the shaded squares. You also may not have the column lying down if a die at either end is over a shaded area. However, the column can span one of the shaded squares. That is, if the die at one end is on a white square, and the die at the other end is on a white square, then it’s alright for the die in the middle to be over a shaded square.

The shortest solution takes 20 moves.

A Rolling-Column Maze from GAMES Magazine

This maze appeared in GAMES in the issue of March, 2003. Click here for the diagram, then print it. The rules are similar to those in Adrian Fisher’s Chasm Maze, except this maze does not use the spanning rule. Here, no part of the column can lie on a barrier.

The shortest solution takes 33 moves.

Richard Tucker’s Rolling-Megalith Maze

Good grief !! These blocks keep getting bigger. But the layout for this maze is rather minimal. Richard Tucker designed a diagram of only 8x8 squares that is almost bare. It has only three barriers.

The maze uses a block of six dice taped together to form a 3x2x1 block. Click here to get to the maze and then print it. Place the block so it is standing on one of its long edges, and it lies across the three squares marked Start. The object is to roll the block until it stands on a long edge and lies across the three squares marked Goal. No part of the block can land on any of the squares with the brick pattern.

Solving this maze is an interesting experience. After you leave Start you travel for a long distance without having to do much thinking. The only false paths you encounter are very short. Then, after the 18th move, the maze suddenly opens up and you’re overwhelmed with false paths and loops. Something similar happens if you solve the maze backwards from Goal. Here you go for 20 moves before you encounter any complexity.

Richard Tucker tells me that the shortest solution is 59 moves. But you should be happy if you can find any solution. So far, the shortest solution I’ve found is 67 moves.

You might have noticed that there’s an interesting trend with these mazes: the bigger the block is, the more complex the maze can be. I think this 3x2x1 block may actually make things too complex. It makes it difficult to see what is going on in the maze. Surely no one would want to make a maze with a block that’s larger than this. Well, someone did. He’s James Stephens, and his web site can be found here. He has a few rolling-block mazes, some of which use blocks of monstrous proportions: 3x3x2, 4x3x2, and 10x1x1. I’m sure no one will try these mazes, but if anyone is foolish enough to make the attempt, then I’m sure no one will actually solve them.

Erich Friedman’s U Maze

This is the weirdest shape yet. To build this U-shaped block you’ll probably have to glue the dice together. That’s what I did, using epoxy glue, and I got a rather sticky mess. But eventually it dried okay.

If you do build the block, click here to get to the layout and then print it. Lay the U so that it covers the squares marked S-T-A-R-T. Then roll the U around until it lies on the squares marked F-I-N-I-S. No part of the U can lie on any square with the brick pattern. However, the U can straddle one of these squares, as it does at the start. And if the block is upright, creating an arch, then the middle die of the arch can be over a square with the brick pattern.

The shortest solution takes 49 moves.

Andrea Gilbert’s Color Zone Maze

Andrea Gilbert has devised a simple new rule that allows for the creation of many different rolling-block mazes. Her layouts have squares of different colors, but no square is a barrier. Instead, she has this rule: The block must always lie on squares of one color.

Here’s what I think is the best of her Color Zone Mazes. It uses the small two-dice block (2x1x1). The block starts upright on the square marked A and must be rolled across the board until it stands upright on the square marked B. In this particular maze, the block can move onto a red square, but only if it stands upright on the red square.

Click here for a diagram of the maze that you can print. To make printing easier, I changed the blue squares to white and the red squares to gray.

Andrea also created a Java program to implement this and other Color Zone mazes. You can click here to go to Andrea’s program for this maze. The program doesn’t have a 3D view, so it only shows the footprint of the block. But the footprint may be all you need to see what’s going on.

You can also click here to go to Andrea’s program for another of these Color Zone mazes. This one uses a larger block. And click here for many more of these mazes on Andrea’s site.

Erich Friedman’s Ramp Maze

This maze really isn’t as difficult as it looks, and it provides a good introduction to the confusing world of Erich Friedman’s multi-level rolling-block mazes. The picture below is a three-dimensional representation of the maze. Click here for a two-dimensional diagram, which you can print. You can roll the block on the two-dimensional diagram as you solve the maze.

This maze uses the three-dice (3x1x1) block, shown here in red on its starting position. (On the two-dimensional diagram, start the block in the upright position on the square marked S.) The object is to roll the block until it is upright on the square marked F.

At first, the block can roll only on the white squares. The light gray squares act as obstacles. However, the block can roll up and down the dark gray ramp. (As the block moves onto the ramp, one end might be on the ramp and the other end can be on a white square or on a light gray square. Don’t worry that the block won’t always be— figuratively—flush with the ramp.)

After you’ve gone up the ramp, things are different. The block now rolls on the top of the light gray squares. You cannot make a move that will send the block crashing down onto the white squares. You also cannot have the die at either end of the block dangling over a white square. However, the block can span a chasm (as it could in Adrian Fisher’s Chasm Maze). If the die at one end is on a light gray square, and the die at the other end is on a light gray square, then it’s alright for the die in the middle to be suspended over a white square.

Erich Friedman’s Multi-Level Maze

I’ll end this section with one of Erich Friedman’s multi-level mazes. These mazes are the most complex expression of the rolling-block idea.

In the maze shown here, only the red blocks are capable of movement. The gray blocks are fixed—they are just part of the landscape. The red blocks move as in normal rolling-block mazes, but they must stay on the level they begin on. So the block made of four dice can only roll on the bottom level. The block made of two dice can only roll on the second level. When it lies horizontal, it must be supported by a block under each of its dice. The red block made of a single die can only roll on the third level. The object is to roll the single-die block onto the third level above the square marked F.

This maze first appeared on my web site in July, 2000. At that time all we had was the diagram. There was no model available, so we couldn’t roll real physical blocks. And we didn’t have a program, so we couldn’t even roll virtual blocks. The mazes had to be solved in the abstract. That was no problem for Friedman and many of the people who solve his puzzles, because they prefer to keep things abstract. But I can’t work a puzzle like that, and I suspect most people are like me. But now we have both a wooden model and a program for the multi-level mazes.

First the program: It is a 3D Java program written by Andrew Fenwick when he was a student at the University of Warwick in England. At the time he was exploring various aspects of rolling-block mazes. The program presents an angled view from above that allows you to see what the blocks look like and, at the same time, see the entire maze. The picture at the right is a screen shot of the program.

Andrew had his program running on the University’s web site, but because he has now graduated, he could no longer keep the program on that site. He kindly gave me permission to move the program to my web site. You can find it here. It implements six multi-level mazes.

And now, the wooden model: It is designed by Kate Jones, whose company Kadon has turned many puzzles and games into intriguing, playable sculptures. Kate has put a page on Kadon’s web site to describe this set. You can click here for the page. There are no pointers from her site to the page, so only we maze enthusiasts will know about it.

I bought a set from Kadon and it’s shown here. Having pieces you can actually hold and roll around the board makes the puzzle more pleasurable. It even makes the puzzle easier to solve. I usually leave the set on the coffee table, and it actually impressed some non-puzzle people who were over at the house.

And speaking of models of rolling-block mazes . . .

Here is a design by puzzle creator Oskar van Deventer. It’s for a hand-held device that will play many types of rolling-block mazes. This design has not been built or published, and it may never be, but it’s intriguing. Oskar creates devices that facilitate movement through a puzzle and, at the same time, enforce the rules of the puzzle.

The red tiles can be placed on the board to form barriers. The silver blocks are various rolling blocks. Notice the clever way that the block closest to the top of the picture could implement Adrian Fisher’s Chasm Maze (the ends of this 3x1x1 column will not move onto the red tiles, but the pin at the center of the column can pass over a tile). The strange cube shown inside the maze—the cube with an antenna on top—implements one of my mazes. The original version of that maze is shown here. A single die is used in the original version, and the rule is that a 1 cannot appear on top of the die. The antenna enforces that rule, because the face opposite the antenna can never be on top. There is other equipment here that can’t be explained, because they enforce rules that we haven’t even tried out in a maze.

If you have a company that builds hand-held puzzles, you might contact Oskar or me. You can use this address: .

To the rolling-CUBE mazes

Back to the home page